√99以上 相似 問題 難問 132036
19 (H31)年度公立高校入試・正答率が低い難問③ 今回は、19年度の公立入試問題の中で、正答率が低かった問題を詳紹介する。 なお、19年度9月1日現在、正答率が公式に発表され、問題がインタネット上で公開されているもののみ扱う。 ※年3月まで
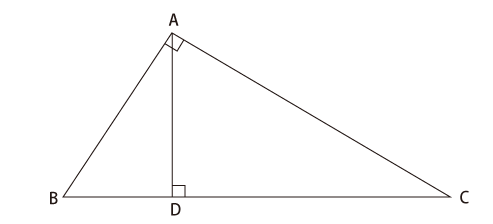
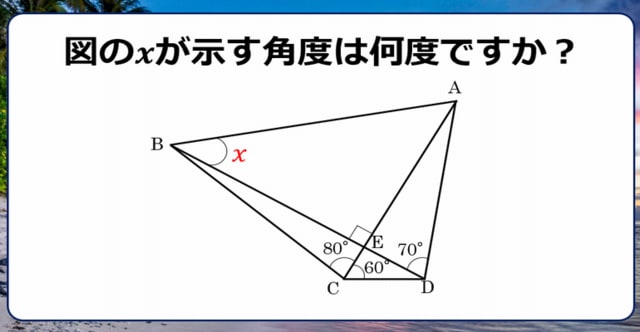
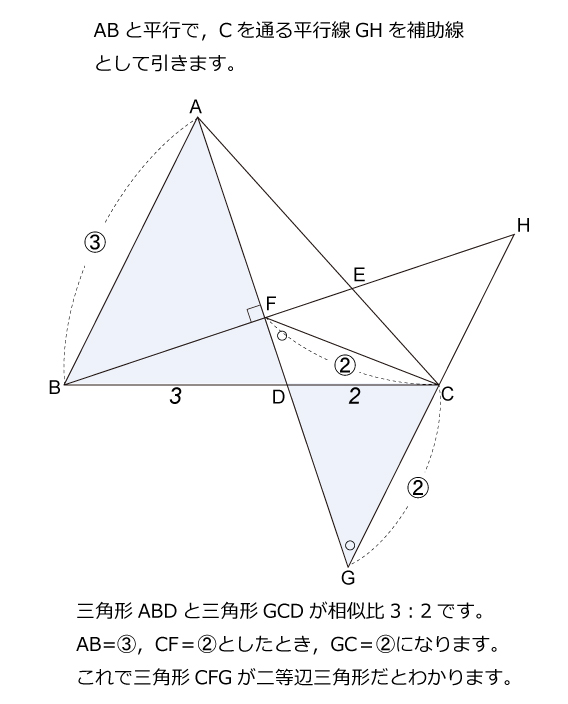
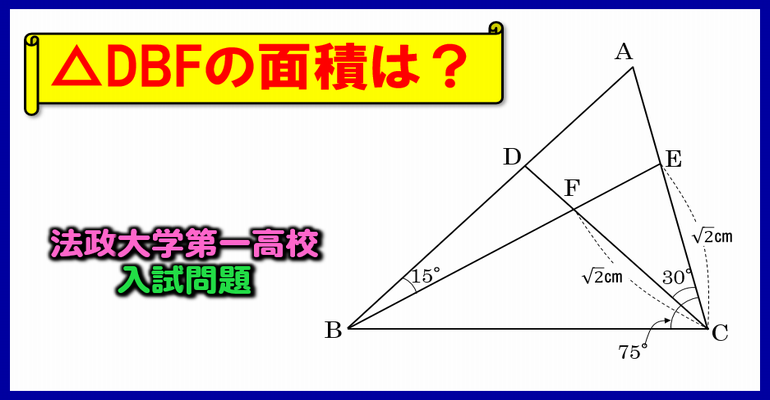
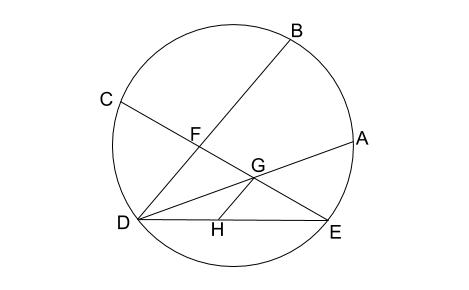
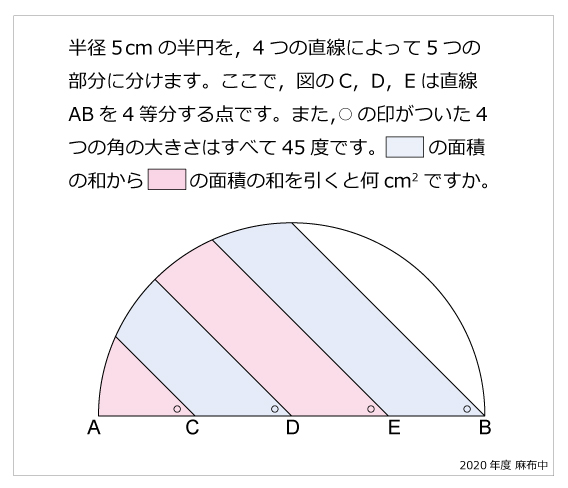
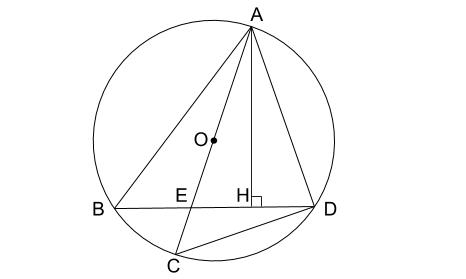
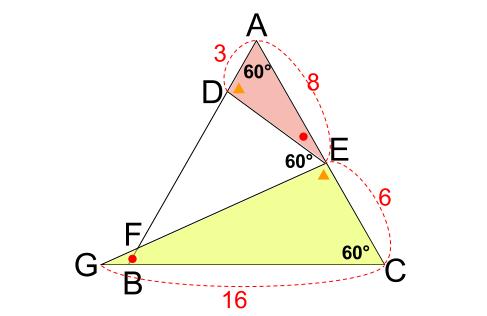
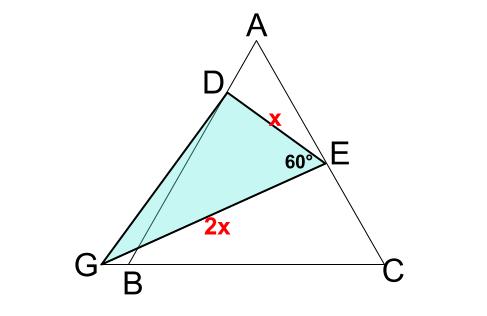
相似 問題 難問-5相似な図形 122 章末問題 1 レベル2 1 次の図で,xの値を求めよ。 ⑴ ⑵ ⑶ 〔土浦日大高 〕 〔 〔大阪産業大附高 神奈川県独自〕 4 右の図は,3 つの長方形 adeb ,befc,cfda を側面とし, ∠a=∠d=90° の2 つの直角三角形 abc ,def を底面とする三角柱で ある。また,g ,h はそれぞれ辺②2 de ea = bd ba;
相似 問題 難問のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 | ||
 |  |  |
 |  |  |
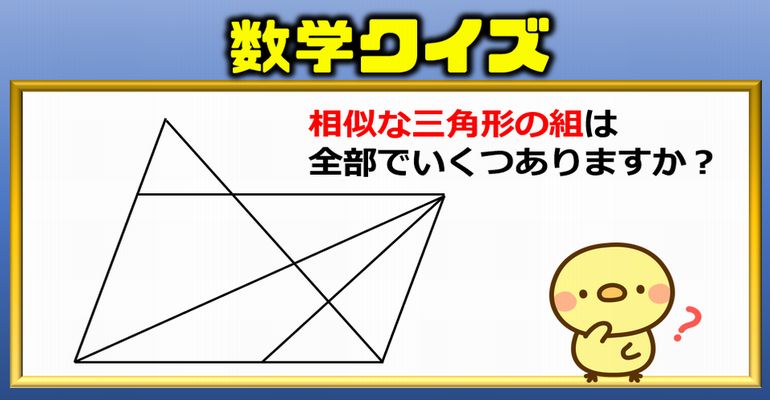
「相似 問題 難問」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 |  | |
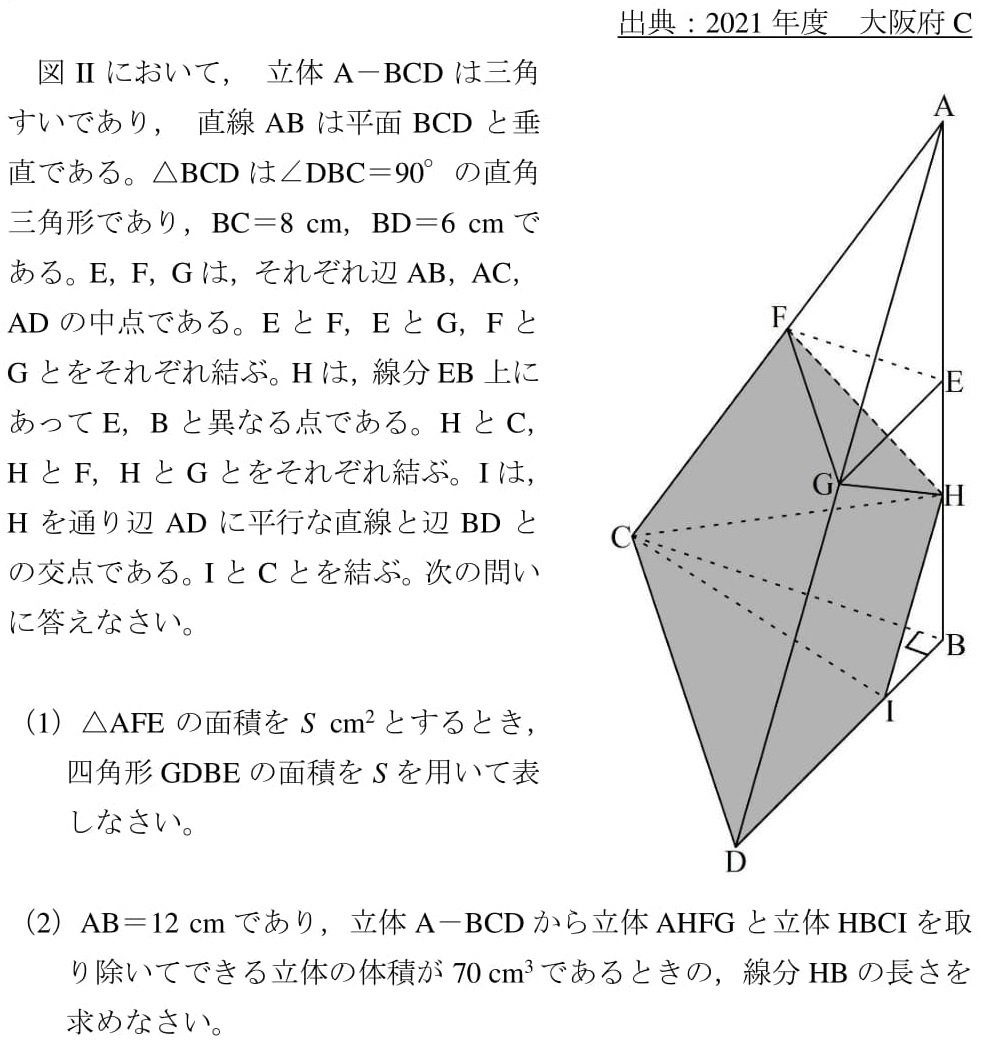
「相似 問題 難問」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
 |  | 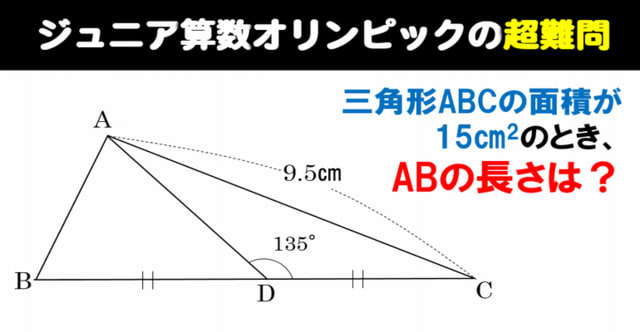 |
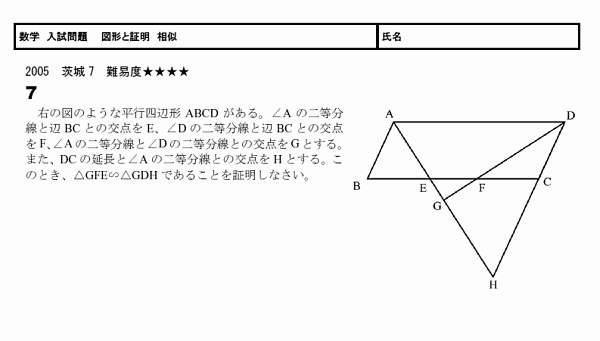
「相似 問題 難問」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
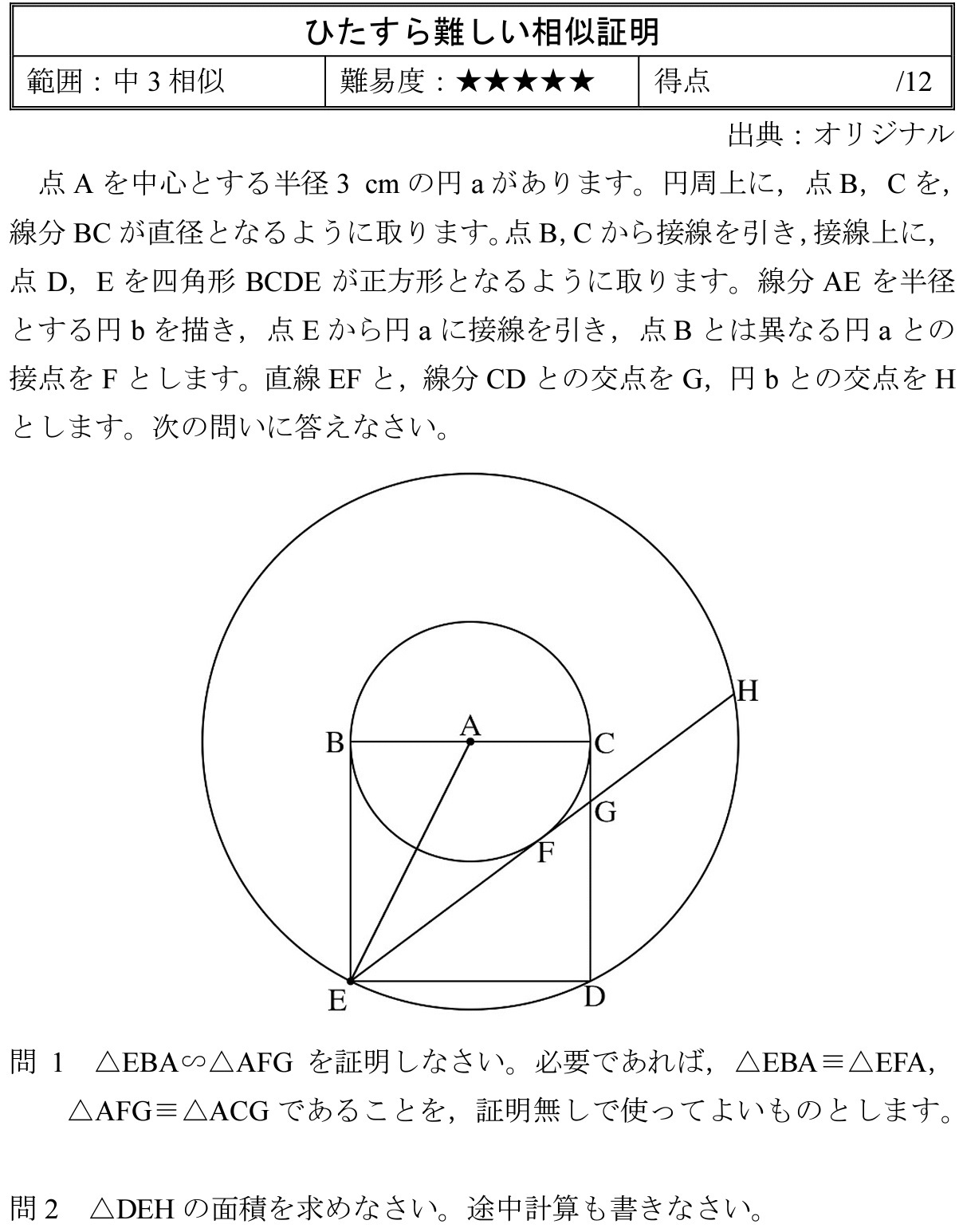 |  | |
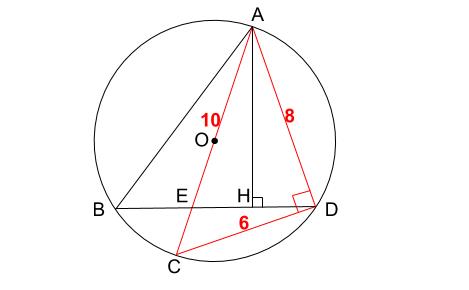 |  |  |
 | ||
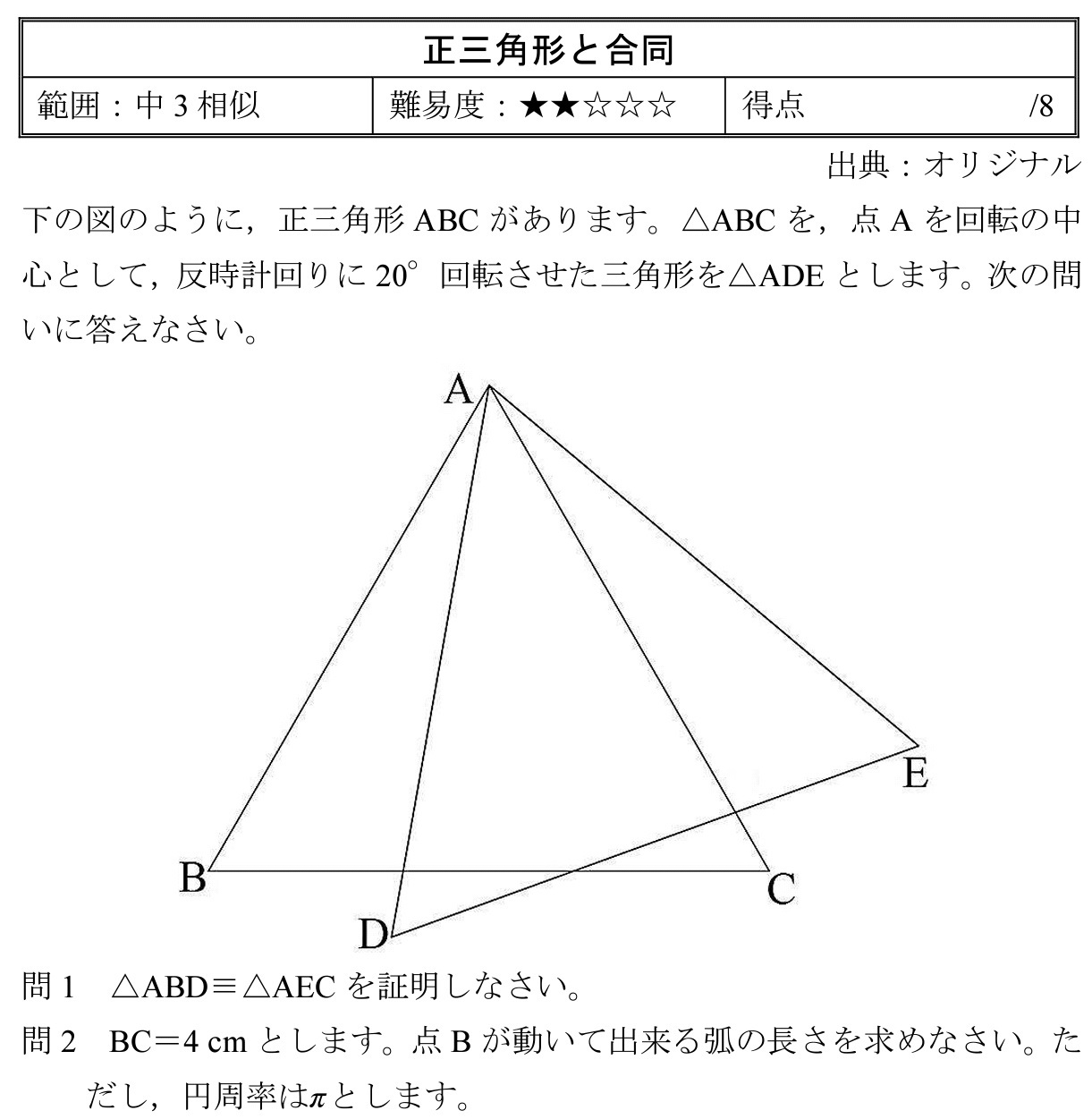
「相似 問題 難問」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「相似 問題 難問」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  | |
「相似 問題 難問」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 |  |  |
「相似 問題 難問」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  | |
「相似 問題 難問」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |
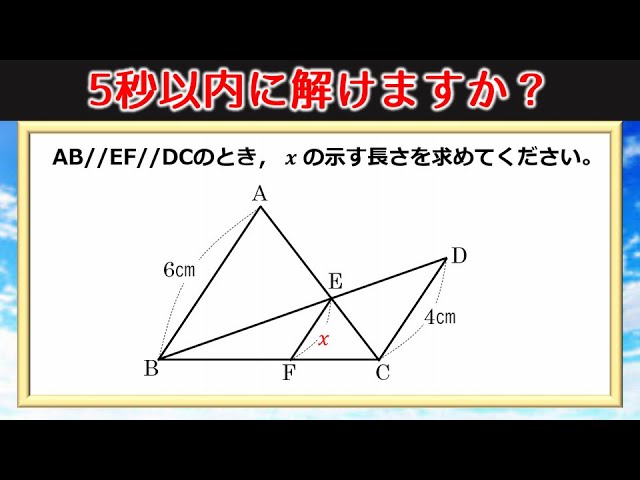
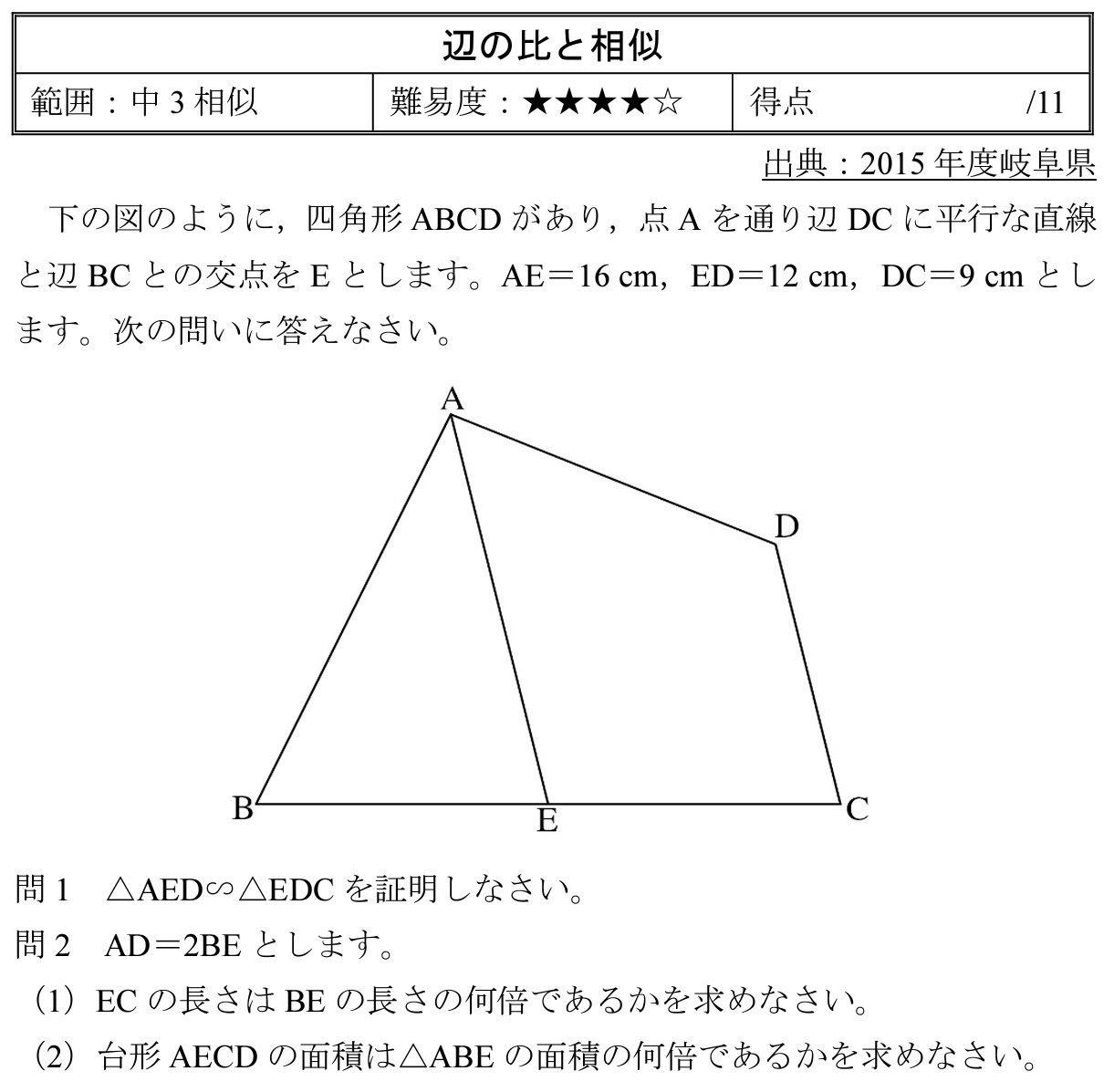
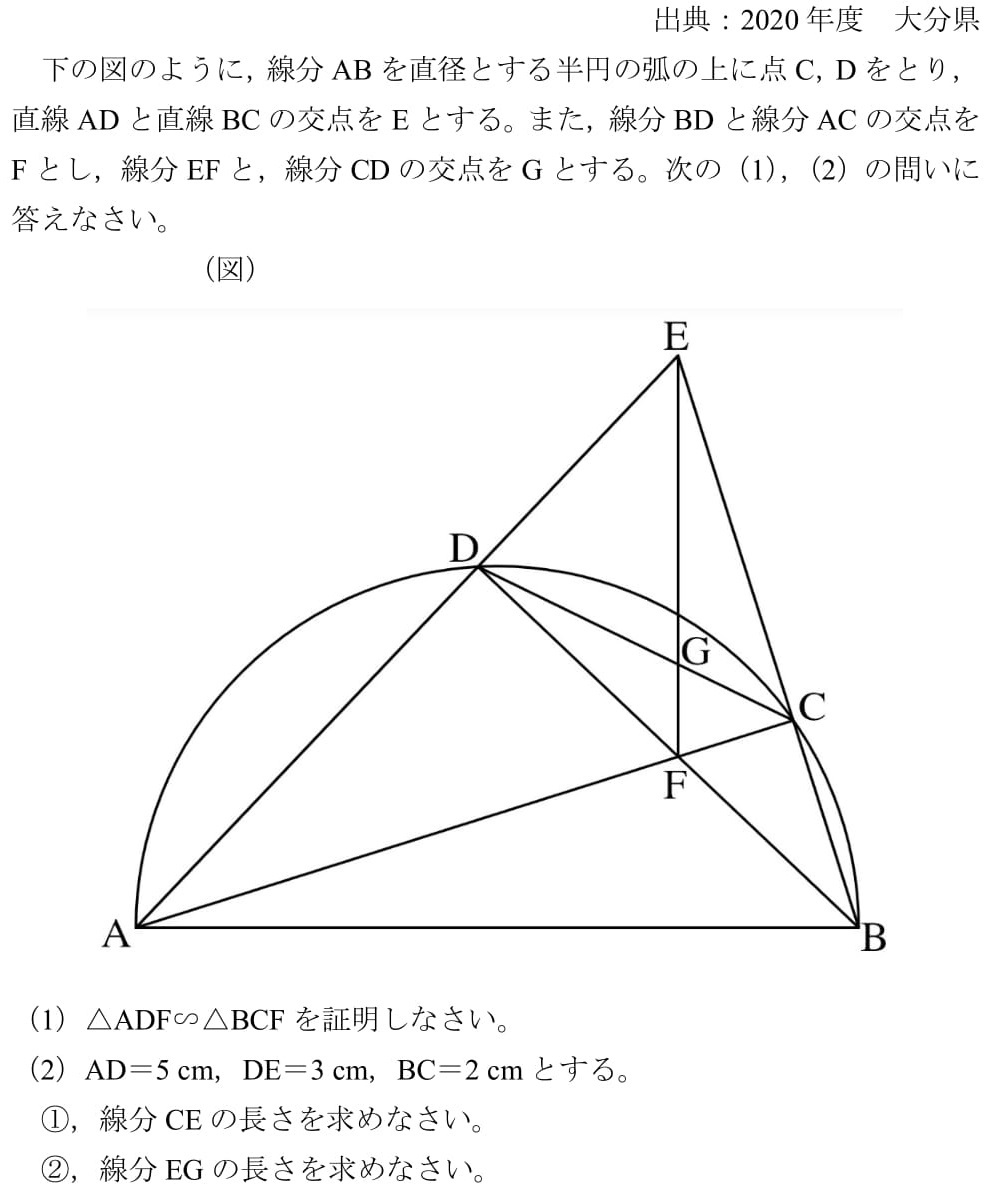
相似比を3乗することで求めてやることができます。 つまり 相似比がわかれば 体積比はすーぐに求めることができるということですね! それでは、さっきの円錐の問題を考えてみましょう。 円錐問題の考え方 円錐を2つに分けた図形の体積比を考えるの 今回はある裏技をご紹介したいと思います(*´ω`*) 後ほど簡単な例題も紹介するので、そちらもぜひ見ていって下さい~ 裏技の説明 証明 ① adcと cbeの相似 ② 面積比 a b ③ aedと abeと ebc ④ dec 例題 問題 答え まとめ 裏技の説明 それでは詳しく見ていきます。 この裏技が使えるのは、台形の上底と下底の長さか、比が分かっているときのみです。 平行でない
コメント
コメントを投稿